3. Using objectives in constraint programming: the Golomb Ruler Problem

In this chapter, we are not only looking for a feasible solution but we want the best solution! Most of the time, the search is done in two steps. First, we find the best solution[1]. Second, we prove that this solution is indeed the best (or as good as any other feasible solution in case there are multiple optimal solutions) by scouring (preferably implicitly) the complete search tree.

Overview:

We start by stating the Golomb Ruler Problem (GRP) and showing that this problem is difficult. We implement five models and compare them two by two. To do so, we introduce some basic statistics about the search (time, failures, branches, ...). Two very useful techniques are introduced: adding better bounds and breaking symmetries. Finally, we say a few words about the strategies used by the solver to optimize an objective function.

Prerequisites:

• Basic knowledge of C++.
• Basic knowledge of Constraint Programming (see chapter Introduction to constraint programming).
• Basic knowledge of the Constraint Programming Solver (see chapter First steps with or-tools: cryptarithmetic puzzles)

Remarks:

• The sums used in this chapter to model the GRP are tricky but you don’t need to master them. We do all the dirty work for you. In fact, you can completely skip them if you wish. The basic ideas behind these sums are simple and are easy to follow.
• We introduce two kinds of variables in our modelizations: the marks of the ruler and the differences between the marks.
• When written, this chapter improved each algorithm one section after the other. Since then, the compiler has been partly rewritten and the algorithms now have different efficiencies. You can read more about their updated efficiencies in the section First results of the section Default search.

Classes under scrutiny:

AllDifferent, OptimizeVar, SearchLimit.

Files:

The files used in this chapter are:

• golomb1.cc: A first implementation. We show how to tell the solver to optimize an objective function. We use the 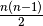differences as variables.
• golomb2.cc: Same file as golomb1.cc with some global indicators about the search and the use of DebugString().
• golomb3.cc: Same file as golomb2.cc with some global statistics and the use of SearchLimits.
• golomb4.cc: A second implementation. This time, we only use the marks as variables and introduce the quaternary inequality constraints.
• golomb5.cc: We improve the second implementation by reintroducing the 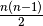differences variables.
• golomb6.cc: In this third implementation, we replace the inequality constraints by the more powerful globlal AllDifferent constraint.
• golomb7.cc: The last implementation is a tightening of the model used in the third implementation. We add better upper and lower bounds and break a symmetry in the search tree.

In all the codes, we use the same strategy to select the next variable to branch on (CHOOSE_FIRST_UNBOUND) and the same strategy to assign it a value (ASSIGN_MIN_VALUE). The times we compare not only measure the solve process but also the time needed to construct the model.

Content:

• 3.1. Objective functions and how to compare search strategies
• 3.2. The Golomb ruler problem and a first model
  • 3.2.1. Description of the problem
  • 3.2.2. How to solve the problem?
• 3.3. An implementation of the first model
  • 3.3.1. An upper bound
  • 3.3.2. The first model
• 3.4. What model did I pass to the solver?
  • 3.4.1. Inspect objects with DebugString()
  • 3.4.2. Use the default flags
• 3.5. Some global statistics about the search and how to limit the search
  • 3.5.1. Time
  • 3.5.2. Failures
  • 3.5.3. Branches
  • 3.5.4. SearchLimits
• 3.6. A second model and its implementation
  • 3.6.1. Variables
  • 3.6.2. Constraints
  • 3.6.3. An improved version
• 3.7. A third model and its implementation
• 3.8. How to tighten the model?
  • 3.8.1. Breaking symmetries with constraints
  • 3.8.2. Better bounds helps
• 3.9. How does the solver optimize?
• 3.10. Summary

Footnote

[1]

How do we know we have a best solution? Only when we have proven it to be so! The two steps are intermingled. So why do we speak about two steps? Because, most of the time, it is easy to find a best (good) solution (heuristics, good search strategies in the search tree, ...). The time-consuming part of the search consist in disregarding/visiting the rest of the search tree.