3.7. A third model and its implementation

1. C++ code:
   1. golomb6.cc

By using the same variables Y[i][j] = X[j] - X[i] in our improved version of our second model in the previous section, we were able to couple the effect of the propagations of the “quaternary constraints”. But these constraints lack a global vision of the propagation and this is were the global AllDifferent constraint comes into the picture.

Let’s replace the quaternary constraints by the AllDifferent constraint on the Y variables:

std::vector<IntVar*> Y;
for (int i = 1; i <= n; ++i) {
  for (int j = i + 1; j <= n; ++j) {
    IntVar* const diff = s.MakeDifference(X[j], X[i])->Var();
    Y.push_back(diff);
    diff->SetMin(1);
  }
}
s.AddConstraint(s.MakeAllDifferent(Y));

and compare our three implementations, again to compute :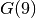

Statistics	Impl1	Impl2	Impl2+	Impl3
Time (s)	4,712	48,317	1,984	0,338
Failures	51 833	75 587	53 516	7 521
Branches	103 654	151 169	107 025	15 032
Backtracks	51 836	75 590	53 519	7 524

What an improvement! In the next section, we present two strategies that generally allow to tighten a given model and thus improve, sometimes dramatically, the search time.