9. Travelling Salesman Problems with constraints: the TSP with time windows

The third part of this manual deals with Routing Problems: we have a graph[1] and seek to find a set of routes covering some or all nodes and/or edges/arcs while optimizing an objective function along the routes[2] (time, vehicle costs, etc.) and respecting certain constraints (number of vehicles, goods to pickup and deliver, fixed depots, capacities, clients to serve, time windows, etc.).

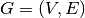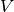[1]	A graph is a set of vertices (the set ) connected by edges (the set 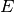). A directed edge is called an arc. When we have capacities on the edges, we talk about a network.

[2]

The transportation metaphor is helpful to visualize the problems but the class of Routing Problems is much broader. The Transportation Problem for instance is really an Assignment Problem. Networks can be of any type: telephone networks (circuit switching), electronic data networks (such as the internet), VLSI (the design of chips), etc.

To solve these problems, the or-tools offers a dedicated Constraint Programming sub-library: the Routing Library (RL).

The next two chapters each deal with one of two broad categories of Routing Problems:

• The chapter Travelling Salesman Problems with constraints: the TSP with time windows deals with Node Routing Problems where nodes must to be visited and served.
• The chapter Vehicule Routing Problems with constraints: the capacitated vehicle routing problem deals with Vehicle Routing Problems where vehicles serve clients along the routes.

These three categories of problems share common properties but they all have their own paradigms and scientific communities.

In this chapter, we’ll discover the RL with what is probably the most studied problem in Operations Research: the Travelling Salesman Problem (TSP)[3].

[3]	We use the Canadian (and British, and South African, and...) spelling of the verb travelling but you’ll find much more scientific articles under the American spelling: traveling.

We use the excellent C++ ePiX library[4] to visualize TSP solutions in TSPLIB format and TSPTW solutions in López-Ibáñez-Blum and da Silva-Urrutia formats.

[4]	The ePiX library uses the engine to create beautiful graphics.

Overview:

We start this chapter by presenting in broad terms the different categories of Routing Problems and describe the Routing Library (RL) in a nutshell. Next, we introduce the Travelling Salesman Problem (TSP) and the TSPLIB instances. To better understand the RL, we say a few words about its inner working and the CP model we use. Because most of the Routing Problems are intractable, we use Local Search. We explain our two phases approach in details and show how to model the TSP in a few lines. Finally, we model and solve the TSP with Time Windows.

Prerequisites:

• Basic knowledge of C++.
• Basic knowledge of Constraint Programming (see the chapter Introduction to constraint programming).
• Basic knowledge of the Constraint Programming Solver (see the chapter First steps with or-tools: cryptarithmetic puzzles).
• Basic knowledge of Local Search (see the chapter Local Search: the Job-Shop Problem).

Files:

You can find the code in the directory documentation/tutorials/cplusplus/chap9.

The files inside this directory are:

• tsp.h: This file contains the TSPData class that records the data for the TSP. This file is used throughout the TSP examples.
• tsplib.h: Declarations of TSPLIB keywords and the TSPLIBDistanceFunctions class.
• tsp_epix.h: This file provides the helper functions to visualize TSPLIB solutions with the ePiX library.
• tsplib_solution_to_epix.cc: A simple program to visualize solutions in TSPLIB format with the ePiX library.
• tsp_minimal.cc: A minimalist implementation of the TSP with the RL.
• tsp.cc: A basic implementation of the TSP with the RL.
• tsp_forbidden_arcs.cc: The TSP with forbidden arcs between some nodes.
• tsptw.h: This file contains the TSPTWData class that records the data for the Travelling Salesman Problem with Time Windows. This file is used throughout the TSPTW examples.
• tsptw_epix.h: This file provides the helper functions to visualize TSPTW solutions with the ePiX library.
• tsptw.cc: A basic implementation of the TSPTW with the RL.
• tsptw_ls.cc: A specialized implementation of the TSPTW with the RL.

Content:

• 9.1. A whole zoo of Routing Problems
  • 9.1.1. Node Routing Problems
  • 9.1.2. Vehicle Routing Problems
  • 9.1.3. Arc Routing Problems
• 9.2. The Routing Library (RL) in a nutshell
  • 9.2.1. Objectives
  • 9.2.2. Out of the box models
  • 9.2.3. On top of the CP library
  • 9.2.4. Local Search
  • 9.2.5. Tuning the search
  • 9.2.6. Dimensions
  • 9.2.7. Disjunctions
  • 9.2.8. Routes/Vehicles are not mandatory
  • 9.2.9. Heterogeneous fleet of vehicles
  • 9.2.10. Costs
  • 9.2.11. Limitations
• 9.3. The Travelling Salesman Problem (TSP)
  • 9.3.1. The Problem
  • 9.3.2. Benchmark data
  • 9.3.3. The TSPData class
  • 9.3.4. Visualization with ePix
• 9.4. The model behind the scenes: the main decision variables
  • 9.4.1. The main idea: the node decision variables
  • 9.4.2. The auxiliary graph
  • 9.4.3. How to switch from NodeIndex to int64 and vice-versa?
  • 9.4.4. How to follow a route?
  • 9.4.5. Not all int64 indices have a corresponding IntVar nexts_ variable
  • 9.4.6. To summarize
• 9.5. The model behind the scene: overview
  • 9.5.1. The RoutingModel class
  • 9.5.2. Variables
  • 9.5.3. Constraints
  • 9.5.4. The objective function
  • 9.5.5. Miscellaneous
• 9.6. The TSP in or-tools
  • 9.6.1. Minimalistic implementation
  • 9.6.2. Basic implementation
  • 9.6.3. How to avoid some edges?
• 9.7. The two phases approach
  • 9.7.1. The initial solution
  • 9.7.2. The PathOperator class
  • 9.7.3. Local Search PathOperators
  • 9.7.4. Filters
  • 9.7.5. A Local Search heuristic for the TSP
• 9.8. The Travelling Salesman Problem with Time Windows (TSPTW)
  • 9.8.1. The Travelling Salesman Problem with Time Windows
  • 9.8.2. Benchmark data
  • 9.8.3. The TSPTWData class
  • 9.8.4. Random generation of instances
  • 9.8.5. Visualization with ePix
• 9.9. The TSPTW in or-tools
  • 9.9.1. Time windows as a Dimension
  • 9.9.2. A basic heuristic to find an initial solution
• 9.10. Summary