10.3. The Capacitated Vehicle Routing Problem (CVRP)

1. C++ code:
   1. cvrp_data.h
   2. check_cvrp_solution.cc
2. Data files:
   1. A-n32-k5.vrp
   2. opt-A-n32-k5

We don’t have much to say about the CVRP as much has been said in the section The Vehicle Routing Problem (VRP). The side constraint we add here to the VRP is a capacity constraint: each vehicle must respect its capacity on the route it traverses, i.e. the sum of the node capacities of all the nodes serviced by one vehicle must be smaller than the vehicule capacity - for all vehicles.

10.3.1. The problem

The Capacitated Vehicle Routing Problem (CVRP) is one class of Vehicle Routing Problems where the vehicles have a certain capacity they can not exceed. A client can only be serviced by one vehicle. The depot is the same for all vehicles and doesn’t need to be serviced.

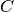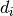In this version, all vehicles have the same capacity that cannot be exceeded on a tour and clients (nodes) have demands. A client has a demand that has to be met when a vehicle services this client. Think of demands as quantities of goods that the vehicle picks up when visiting clients: the total among of goods/demands picked up along the route cannot exceed its capacity.

The program check_cvrp_solution allows you to check if indeed the capacities of the vehicles are respected along the routes. For instance, invoking:

./check_cvrp_solution -log_level=1 -instance_file=A-n32-k5.vrp
                                        -solution_file=opt-A-n32-k5

prints:

Route 1 with capacity 100
 Servicing node 22 with demand 12 (capacity left: 88)
 Servicing node 32 with demand 0 (capacity left: 88)
 Servicing node 20 with demand 24 (capacity left: 64)
 Servicing node 18 with demand 19 (capacity left: 45)
 Servicing node 14 with demand 16 (capacity left: 29)
 Servicing node 8 with demand 16 (capacity left: 13)
 Servicing node 27 with demand 2 (capacity left: 11)
Route 2 with capacity 100
 Servicing node 13 with demand 21 (capacity left: 79)
 Servicing node 2 with demand 19 (capacity left: 60)
 Servicing node 17 with demand 18 (capacity left: 42)
 Servicing node 31 with demand 14 (capacity left: 28)
Route 3 with capacity 100
 Servicing node 28 with demand 20 (capacity left: 80)
 Servicing node 25 with demand 24 (capacity left: 56)
Route 4 with capacity 100
 Servicing node 30 with demand 2 (capacity left: 98)
 Servicing node 19 with demand 1 (capacity left: 97)
 Servicing node 9 with demand 6 (capacity left: 91)
 Servicing node 10 with demand 16 (capacity left: 75)
 Servicing node 23 with demand 4 (capacity left: 71)
 Servicing node 16 with demand 22 (capacity left: 49)
 Servicing node 11 with demand 8 (capacity left: 41)
 Servicing node 26 with demand 24 (capacity left: 17)
 Servicing node 6 with demand 7 (capacity left: 10)
 Servicing node 21 with demand 8 (capacity left: 2)
Route 5 with capacity 100
 Servicing node 15 with demand 3 (capacity left: 97)
 Servicing node 29 with demand 15 (capacity left: 82)
 Servicing node 12 with demand 14 (capacity left: 68)
 Servicing node 5 with demand 19 (capacity left: 49)
 Servicing node 24 with demand 8 (capacity left: 41)
 Servicing node 4 with demand 6 (capacity left: 35)
 Servicing node 3 with demand 21 (capacity left: 14)
 Servicing node 7 with demand 12 (capacity left: 2)
Solution is feasible!
Obj value = 784

As you can see, each vehicle has its capacity respected. In case you wonder, we use the real node identifiers (from the original graph) in this output.

In the next section, we show you how to customize each vehicle (its usage cost, its capacity, its edge traversal cost).

Exact methods can solve instances with 100 clients (see [Roberti2012]) but even heuristics are limited to solve instances with more or less 1200 clients (see [Groër2011]). Most efficient heuristics are a combination of integer programing with local search (see [Toth2008] or [Groër2011]).

[Roberti2012]

R. Roberti. Exact algorithms for different classes of vehicle routing problems, PhD Thesis, University of Bologna, 2012.

[Groër2011]

(1, 2) C. Groër, B. Golden and E Wasil. A Parallel Algorithm for the Vehicle Routing Problem, INFORMS Journal on Computing, v. 23(2), pp. 315-330, 2011.

[Toth2008]

P. Toth and A. Tramontani. An integer linear programming local search for capacitated vehicle routing problems, in The Vehicle Routing Problem: Latest Advances and New Challenges, Springer US, pp. 275-295, 2008.

Several problems modelled as CVRP

[TO BE WRITTEN]

10.3.2. The CVRPData class: part II

To play with instances and see how solutions can change when you change some parts of the instances, the CVRPData class provides some setters:

void SetDepot(RoutingModel::NodeIndex d);
void SetDemand(const RoutingModel::NodeIndex i, int64 demand);
void SetCapacity(int64 capacity);

You even can change the distance between two nodes i and j:

CVRPData cvrp_data(...);
...
RoutingModel::NodeIndex i = ...;
RoutingModel::NodeIndex j = ...;
int64 new_distance = ...;
cvrp_data.SetDistance(i, j) = new_distance;

Note that the call to SetDistance() is different because it returns an lvalue (left value)[1].

You also have the corresponding getters:

RoutingModel::NodeIndex Depot() const;
int64 Demand(const RoutingModel::NodeIndex i) const;
int64 TotalDemand() const;
int64 Capacity() const;
int64 Distance(RoutingModel::NodeIndex i,
               RoutingModel::NodeIndex j) const;

The TotalDemand() method returns the sum of all demands for all clients.

[1]	You don’t need to know the details of what exactly an lvalue is in C++. It’s enough to know that you can use an lvalue in an assignment (to the left of the equal sign).